A turbulent boundary layer greatly increases the drag on a wing, negatively impacting aircraft fuel economy. Unmanned aerial drones in particular experience transition to turbulent flow from the laminar regime at common flight conditions. Transition can be delayed in a number of ways including airfoil geometry and surface actuation to suppress the Tollmien-Schlichting (TS) waves responsible.
The Natural Laminar Flow (NLF) airfoil series is designed to passively delay the growth of TS waves. To actively control the flow instabilities, an array of Piezoelectric-Driven Oscillation Surface (PDOS) actuators are mounted on the suction side of the airfoil. The upstream actuator excites a TS wave at a characteristic frequency, growing and advecting downstream. A second actuator applies a similar disturbance but anti-phase to the upstream one. The destructive interference (wave superposition principle) reduces the TS wave amplitude and growth rate. Mitigation is repeatable with subsequent downstream actuators since the disturbances are amplified by the adverse pressure gradient. Particle Image Velocimetry (PIV) measurements capture several phases of the TS wave progression in the flow through phase-locked and time-averaged velocity fields. Figure 1 shows the locking and mitigation of the TS wave at Window C (a and b, respectively) and Window D downstream (c and d, respectively).
Further developments of this project involve implementing disturbances invoking closed-loop control architectures on a single frequency and a bandwidth of excitable frequencies and to better mitigate the TS wave instabilities. Figure 2a shows the closed-loop control scheme implemented in the experiments. An iterative learning control (ILC) algorithm updates the input signal to the control actuator downstream to mitigate the TS wave over multiple iterations of the control algorithm. Figure 2b shows the trend of the normalized sensor amplitude measured during each test, ultimately ending at approximately 10% of the initial value. The control algorithm is additionally used for experiments with input signals covering multiple frequencies in the excited TS wave range. Figure 3 shows the progression of the hot film sensor signal across ten iterations in the frequency domain. Cases with convergence speed coefficient of ε=0.5 (a) and ε=1.0 (b) are provided. Ultimately, once a robust active wave control system is established, experiments will continue on a swept airfoil model where both TS waves and crossflow instabilities, a mode of transition on swept wings, will be controlled.
Four phases of the TS wave locked by PDOS1 at Window C on the NLF airfoil
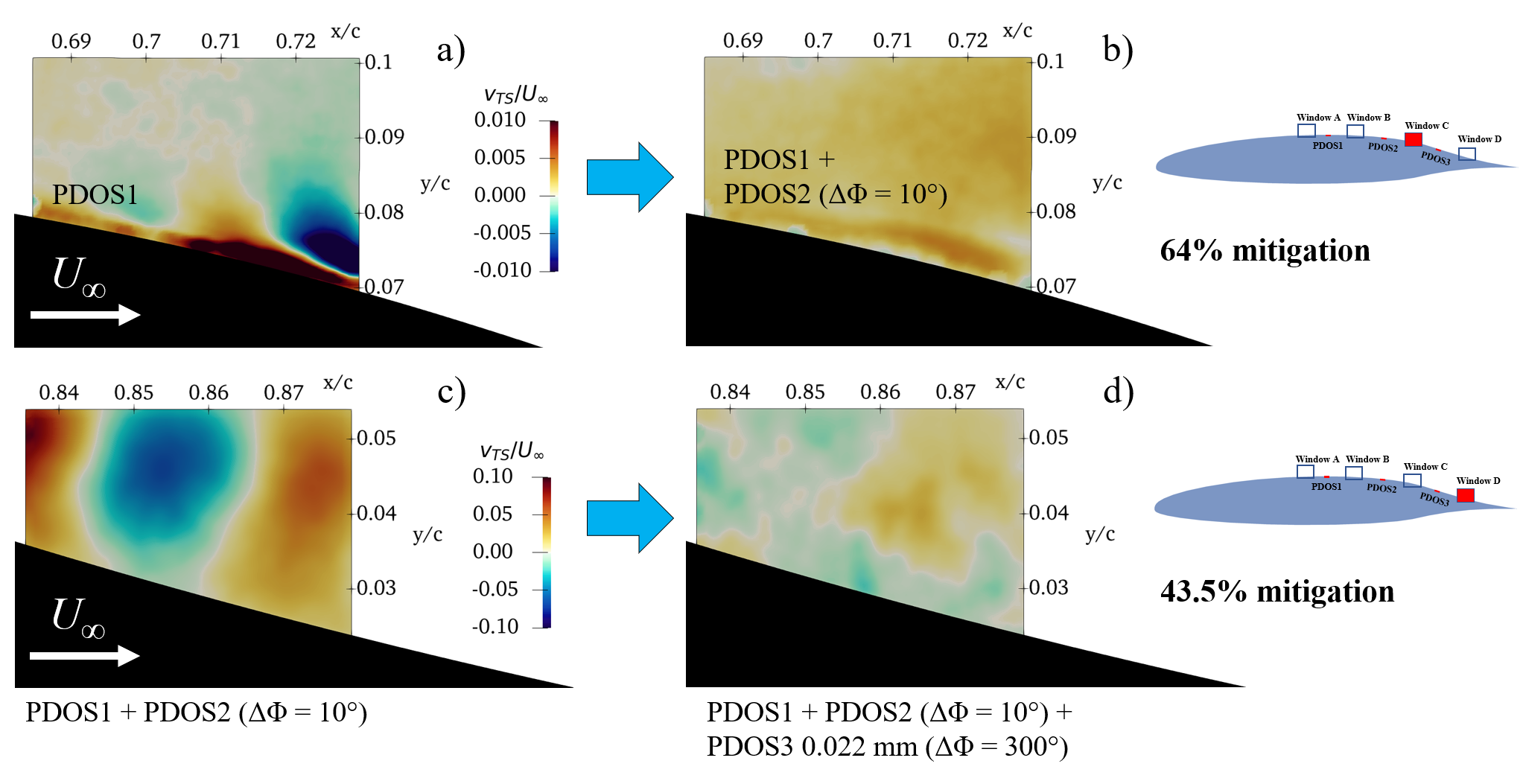
Figure 1: TS wave mitigation at two locations on the NLF0414F airfoil. The velocity fields are colored by the vertical TS wave velocity (time averaged velocity subtracted from velocity fields phase-locked to PDOS actuation).
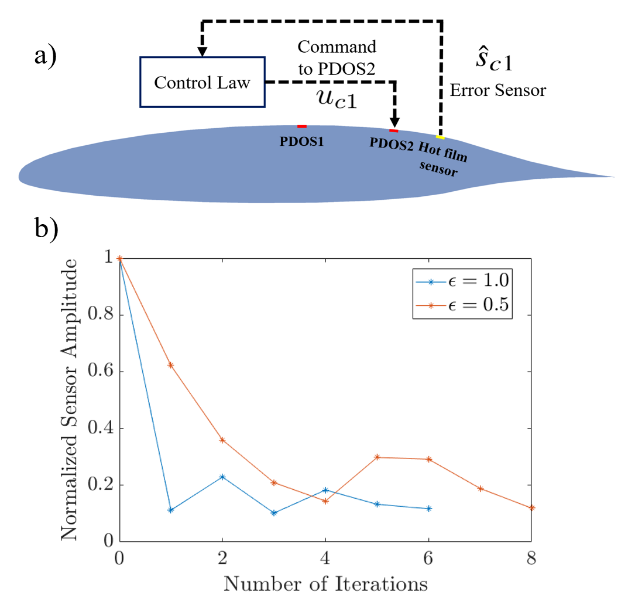
Figure 2: Closed loop control architecture (a) and the variation of normalized amplitude of the hot-film signal with the number of iterations for convergence speed coefficient of ε=0.5 and ε=1.0 (b).
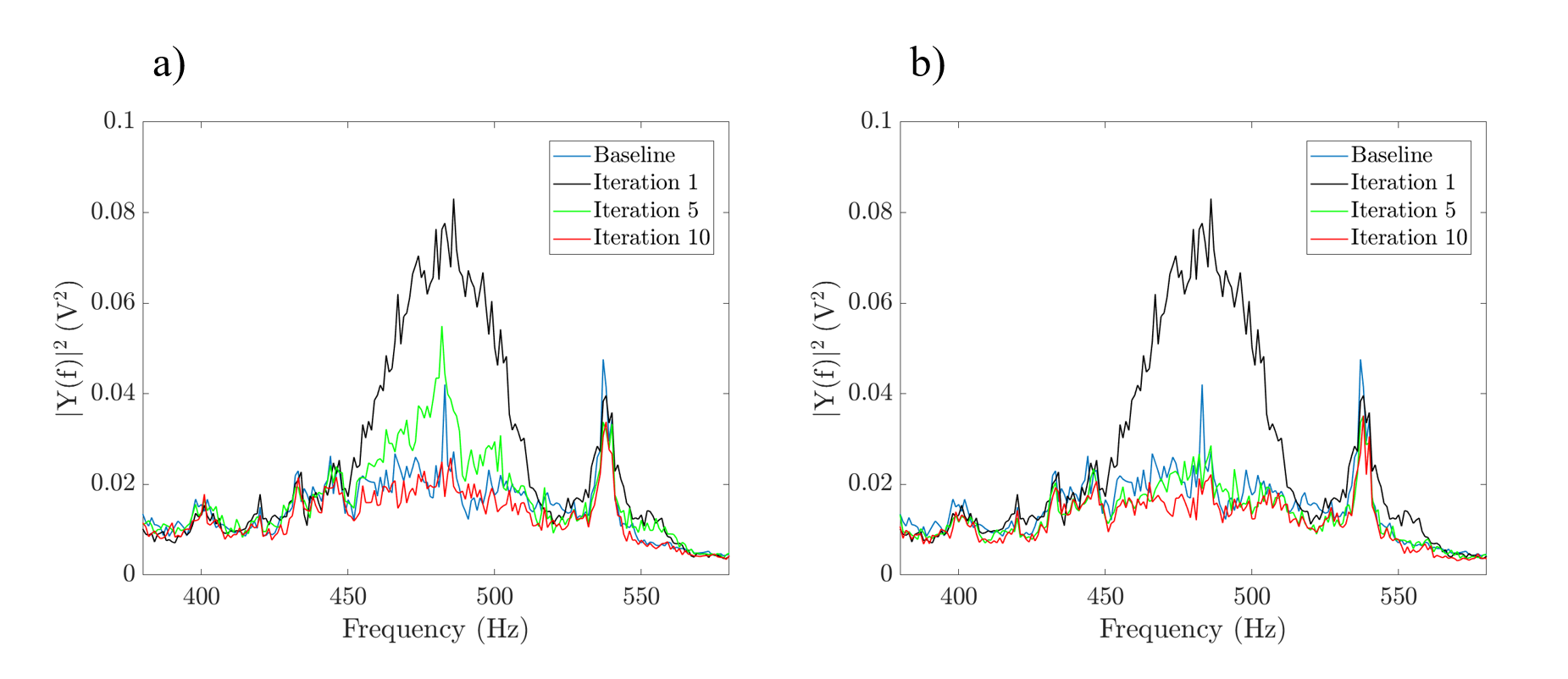
Figure 3: Fast Fourier Transforms of the hot film sensor signal across ten iterations of the ILC algorithm for multiple frequency inputs to the actuators for convergence speed coefficient of ε=0.5 (a) and ε=1.0 (b).
Related Publications:
- Wylie, J. D. B., Mishra, S., and Amitay, M., “Control of Tollmien-Schlichting Waves on a Laminar Airfoil Using Dynamic Surface Modification.” AIAA Journal, final stages of publication, January 2021.
- Wylie, J., Zhao, D., Mishra, S., and Amitay, M., “Control of T-S Waves on a Natural Laminar Flow Airfoil using Dynamic Surface Modification.” AIAA SciTech 2021 Forum, January 2021, https://doi.org/10.2514/6.2021-1547.